「日能研からの挑戦状」～解答・解説付き～

9/27（土）・28（日）に行われる「東海高校・中学校137th記念祭」のパンフレットに、
『日能研からの挑戦状』と称して、記念祭に絡めた算数の問題が載った広告を掲載します。

下の画像をクリックすると問題が拡大します！

解答・解説はコチラ

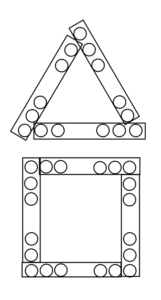
小学生は等間隔に並んで正三角形を作ることが

できるため、人数は３の倍数である。

同様に、中学生は等間隔に並んで正方形を作ることが

できるため、人数は４の倍数である。

つまり、(３の倍数)＋(４の倍数)＝137人という関係が成り立つ。

これを満たす小学生と中学生の人数の組み合わせの1つに、

69＋68＝137がある。

これと、３と４の最小公倍数は12であることを利用して

小学生と中学生の人数の組み合わせの候補を見つけていく。

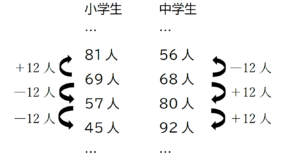
それぞれの組み合わせにおいて、一辺に並ぶ人数を比べる。

・小学生81人、中学生56人のとき

　81÷３＋１＝28(人)

　56÷４＋１＝15(人)　　28－15＝13(人)

　１辺に並ぶ人数は13人違う。

・小学生69人、中学生68人のとき

　69÷３＋１＝24(人)

　68÷４＋１＝18(人)　　24－18＝６(人)

　１辺に並ぶ人数は６人違う。

・小学生57人、中学生80人のとき

　57÷３＋１＝20(人)

　80÷４＋１＝21(人)　　21－20＝１(人)

　１辺に並ぶ人数は１人違う。

・小学生45人、中学生92人のとき

　45÷３＋１＝16(人)

　92÷４＋１＝24(人)　　24－16＝８(人)

　１辺に並ぶ人数は８人違う。

これ以上は１辺に並ぶ人数の差は８人より大きくなるので、小学生45人、中学生92人と分かる。

正解できたかな？